
Hoy voy a explicaros cómo describimos un haz de luz, sea incidente, disperso o como sea.
Antes os recordaré que, en general, se considera “luz” a la parte del espectro electromagnético comprendido entre ciertas longitudes de onda; bueno, para simplificar, a lo que podemos ver con nuestros ojos. Desde el punto de vista de la Física eso no representa una definición estricta, y podemos aplicar nuestros conocimientos de la dispersión en luz visible a ciertos rangos en el infrarrojo y ultravioleta; sobre todo en el infrarrojo (no es que el ultravioleta nos caiga mal, sino que la atmósfera lo absorbe que da gusto). Es decir, la frontera de qué es luz o qué no va a ser algo flexible para nosotros. Tanto mejor.
Una onda electromagnética se llama así porque es una propagación de dos cantidades combinadas: un campo magnético y un campo eléctrico. Ambas cantidades se representan mediante vectores, así que ahí van: E, B. Como veis los he puesto en negrilla, que es como a partir de ahora vamos a escribir los vectores. A veces necesitaré tan sólo el módulo de esos vectores (su longitud, para entendernos), y cuando eso suceda los escribiré sin negrilla: E, B. La relación entre módulos y vectores es E=|E|, y lo mismo para B
Los vectores E y B son siempre perpendiculares, y el plano que forman es a su vez perpendicular a la dirección del movimiento. Es decir, si la onda se dirigiese directamente hacia nosotros veríamos ambos vectores en toda su oscilante magnificencia, siempre cambiantes pero guardando entre sí un ángulo de 90 grados y formando entre ambos un plano perpendicular al movimiento.
Vamos al caso más sencillo: la llamada onda plana. Si nos echásemos a un lado y dejásemos pasar la onda (bueno, y si pudiésemos ver los vectores como flechitas) tendría este aspecto:
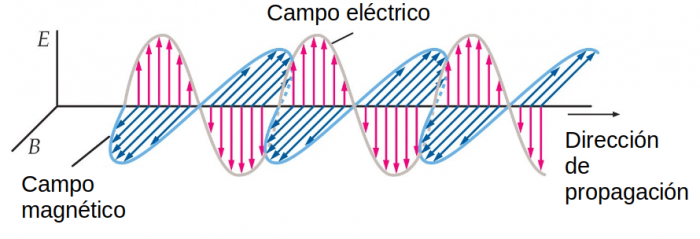
Centrémonos, pues en el vector que nos representa al campo eléctrico E. Dicho vector va cambiando según una onda sinusoidal (en forma de función seno), por lo que podemos escribirla como E=Eo*seno(kx-ωt+φ). La variable “x” representa la posición a lo largo de la dirección de propagación, “t” es el tiempo, Eo es la llamada amplitud de la onda (el valor máximo del módulo del vector campo eléctrico), y las otras tres variables… bueno, mejor cambio la ecuación. Atentos:
E=Eo*sen[2π(x/λ – t/T)+φ]
– λ es la longitud de onda. En el gráfico anterior sería la distancia entre dos crestas de la curva que representa el campo eléctrico.
– T es el período de la onda. Es el tiempo que tarda la onda hacer una sola oscilación, o lo que es lo mismo, en propagarse una longitud λ
Es fácil ver que k=2π/λ y ω=2πt/T. Esas cantidades se conocen como número de onda (k) y frecuencia angular (ω), y resultan bastante útiles. Por ejemplo, nos permiten escribir la onda plana como E=Eo*sen[kx – ωt+φ]. Ah, y la cantidad φ se llama fase. No es que vaya a tener mucha importancia para nosotros. Es un valor fijo, y podemos darle el valor que queramos.
Otra cantidad útil es la frecuencia f, que es la inversa del período: f=1/T. Si el período es el número de segundos que tarda una oscilación, la frecuencia es el número de oscilaciones por segundo. A veces la frecuencia se representa por la letra griega nu (ν), que parece como una uve artística. Para no confundir “nu” con “v” (que suele representar velocidad), voy a usar f a partir de ahora
Para caracterizar una onda de radio puede usarse la frecuencia o el período. Los aficionados a la radioafición hablan de “banda de 12 metros” (en cuyo caso están indicando λ) y las estaciones de radio FM hablan de emisión en 95,2 megahercios (esto es frecuencia). Podemos hacerlo como más nos guste porque hay una forma cómoda de pasar de una a otra. Es esta: λf=v, donde v es la velocidad de propagación de la onda. Cuando son ondas electromagnéticas en el vacío, la velocidad se representa por c, que tiene un valor de 299 729 458 m/s
De acuerdo, tenemos una onda de frecuencia f, longitud λ y velocidad c. Con eso comenzamos a caracterizar una onda plana, pero aún queda algo importante: determinar cómo varía el vector E. En el caso de la onda plana está sencillo. Como puede verse en el dibujo de arriba, un observador que viese venir la onda directamente hacia sí notaría que el vector E va creciendo en la dirección vertical, llegaría a un valor máximo, luego iría decreciendo, se haría cero, volvería a crecer en módulo pero apuntando hacia abajo… vamos, que oscila en la dirección vertical.
Bien, a eso se le llama luz linealmente polarizada. En este caso partículas la dirección de polarización es la vertical, pero en principio puede ser cualquiera. El plano en que oscila el campo E se llama plano de polarización.
Vale, y ¿de qué sirve eso? Pues en el caso de una onda plana bien poco… pero el mundo es más complicado que eso. Habitualmente la luz está generada por gran cantidad de procesos microscópicos. Por ejemplo, al calentar al rojo un trozo de hierro sus átomos vibran y ceden energía en forma de luz. Cada uno de esos átomos emite ondas con diferentes características. Incluso si suponemos que esas ondas tienen todas la misma longitud y frecuencia, cada una tendrá un vector E que apuntará en una dirección distinta, y también las fases φ serán distintas. El resultado será un campo eléctrico bastante despendolado, ya que en general no será una onda plana más que por pura casualidad (o porque hayamos forzado a la luz a comportarse así). Eso significa que, en aplicaciones reales, la onda de luz no será plana y necesitaremos más números para caracterizarla.
Lo primero que vamos a considerar es la intensidad del haz de luz. Esa intensidad recibe varios nombres según la definamos, pero en definitiva va a depender del cuadrado del vector E y será una medida de la energía que tiene la onda. Vamos a llamarla I.
En segundo lugar vamos a fijarnos en su estado de polarización. Es posible, como dije antes, que la luz esté linealmente polarizada si todas las fuentes de luz emiten como ondas planas. Esto es como si un conjunto de personas que van por la calle se pusiesen de acuerdo para andar todos en la misma dirección y siguiendo el paso: posible, no probable. Más habitual es que algunas personas se pongan de acuerdo, y de modo similar la luz puede estar parcialmente polarizada.
¿Cómo medimos ese grado de polarización parcial? La idea es tomar el campo eléctrico E y descomponerlo en dos partes, una de ellas horizontal y otra vertical. En el dibujo anterior todo el campo estaba ya en el eje vertical, pero en general podremos escribirlo como E=Eheh+Evev, donde (eh,ev) son los vectores unitarios (tienen longitud igual a uno por definición) en las direcciones horizontal y vertical.
Cuando tenemos E=Eheh+Evev, podemos escribir la intensidad total como I=|E|2=Eh2 + Ev2
(Aviso a los expertos: sí, ya lo sé, es más complicado que esto, pero me niego a usar cantidades complejas en este punto porque no quiero liarla aún más. Para los no expertos: no hay nada que ver, sigan adelante).
Es decir, la intensidad total será la suma de dos contribuciones, la horizontal y la vertical. Esas dos contribuciones nos dirán cómo de polarizada está la luz. Si Eh=0 o Ev=0 tenemos luz linealmente polarizada. Si, por el contrario, Eh, Ev valen lo mismo y fluctúan al azar (es decir, van cambiando con el tiempo de modo aleatorio), no habrá polarización alguna y tendremos luz natural.
Ahora tengo que añadir un aviso así que QUIETOPARAO. Este es uno de esos casos en que el habla cotidiana difiere del lenguaje de los científicos (más sobre nuestro curioso lenguaje aquí y aquí). “Natural” suele tomarse en el habla cotidiana como antónimo de “artificial”, de modo que luz natural será la del Sol y luz artificial la de las bombillas. Aquí NO usaremos esa convención. Luz natural será luz no polarizada en absoluto, sin importar su origen.
Vale, tenemos ya los dos casos extremos de polarización: total y para nada. Es razonable pensar que habrá casos intermedios.
Si la suma Eh2 + Ev2 nos indica la contribución de las componentes horizontal y vertical del campo eléctrico, su diferencia Eh2 – Ev2 es un indicativo de si una de esas componentes predomina sobre la otra, es decir, de si hay algo de polarización. Vamos a usar esa diferencia para describir la “cantidad de polarización lineal”. Lo designaremos con la letra Q y lo llamaremos… bueno, no le pondremos nombre, vamos a dejarlo en Q.
La cantidad Q describe el grado de polarización, pero no del todo. El problema es que esas cantidades Eh, Ev que hemos considerado no son números reales sino complejos. Los complejos son números con parte real y parte imaginaria, y aunque no voy a explicarlos aquí (para eso está la wikipedia) sí os diré que, debido a ello, necesitamos otra cantidad que me describa la polarización. Bien, lo que hacemos es algo parecido, sólo que en lugar de las componentes horizontal y vertical del campo eléctrico tomamos las componentes en las direcciones de +45º y -45º. Es decir, vemos cuánto campo eléctrico está alineado en la dirección oblicua (formando ángulo de 45º con la horizontal) y cuánto en la “antioblicua” (en dirección formando ángulo de 135º, o lo que es lo mismo, -45º)
De ese modo obtenemos una cantidad similar a la Q que hemos visto antes. La llamaremos U.
Y nos queda una cosa más. Para entenderla imaginemos que la luz no está linealmente polarizada. Eso significa que, si la luz se dirige hacia nosotros, vemos cómo el vector E permanece en un plano perpendicular al de propagación pero va cambiando de dirección en ese plano; es decir.. ¿Pero en qué sentido, horario o antihorario? Para eso necesitamos una cuarta cantidad, que llamaremos V. Según valga V la polarización será levógira o dextrógira (es decir, E irá girando en sentido antihorario u horario)… o mitad carne mitad pescado).
Resumiendo mucho, tenemos cuatro cantidades (I, Q, U, V) que nos representan:
– I la intensidad total
– Q la diferencia entre luz polarizada horizontalmente y verticalmente
– U la diferencia entre luz polarizada a -45º y a -45º
– V la diferencia entre luz polarizada circularmente a derechas y a izquierdas
En ocasiones, por puro afán de simplificación se suele dividir todo por I. De ese modo, ese “paquete” quedará en la forma (1, Q/I, U/I, V/I). La ventaja ahora es que Q/I, U/I y V/I tienen valores comprendidos entre -1 y +1, y de hecho ni siquiera tienen unidades, así que una complicación menos.
A ese “paquete” (I, Q, U, V) se le conoce como vector de Stokes. Sí, vector. Estarás acostumbrado, amigo lector, a pensar en un vector como una flechita. Esa es la forma en que la usamos para describir fuerzas o velocidades, pero lo cierto es que “vector” puede ser cualquier cosa que cumpla un cierto conjunto de propiedades matemáticas. Además, los físicos somos así de chulitos, y si queremos llamar vector a eso, pues lo hacemos y ya está.
Lo importante aquí es que el estado de una onda electromagnética como la de un haz de luz viene determinada, a los efectos que no interesa, por su vector de Stokes. Cuando en la entrada anterior describí el proceso de dispersión como B=P*A, tanto A como B son vectores de Stokes.
¿Y qué es P? Eso representa lo que la partícula le hace al haz de luz para dispersarlo. Pero eso lo veremos otro día.
Resumen para dummies. La luz es una onda electromagnética y sus vibraciones se caracterizan por frecuencia y longitud de onda. La forma particular de vibración que tiene un haz de luz puede indicarse mediante su vector de Stokes, un conjunto de cuatro componentes que nos indican la intensidad y su tipo de polarización.
[Etiquetas: scattering 101]
Deja una respuesta