
En la anterior entrada vimos cómo la luz se puede representar mediante el llamado vector de Stokes (I,Q,U,V). Sigamos a partir de ahí.
Cuando la luz pasa por un sistema que cambia su estado (por ejemplo, tras chocar con una partícula), su vector de Stokes cambia. La relación entre ambos vectores viene dada mediante la llamada matriz de Müller. En lenguaje compacto podemos escribirlo como Is=P*Ii, donde Ii, Is son los vectores de Stokes de la luz incidente y dispersada. Para ser más exacto, deberíamos poner algo del tipo Is=c*P*Ii, donde c es una constante de normalización que da cuenta, por ejemplo, del hecho de que la intensidad de una onda electromagnética decrece con el cuadrado de la distancia. Es algo que no hemos considerado, y que aquí no tiene mucha importancia.
Vamos a escribirlo en notación más amplia, y si me lo permite dejaremos al margen las constantes de normalización para que la cosa quede más simple:
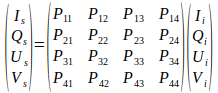
Si os parece, vamos a ver algunos ejemplos y así aprenderéis a jugar con las matrices.
En primer lugar, vamos a hacer luz polarizada. Supongamos que tenemos un haz de luz inicialmente natural (es decir, sin polarizar) y queremos convertirla en luz polarizada. Los fotógrafo usan filtros polarizadores, lo que les permite por ejemplo eliminar reflejos. Con ello filtran la luz dejando pasar solamente aquellas vibraciones que oscilan en una dirección determinada (llamada dirección de polarización, o eje de transmisión.
Supongamos que queremos luz polarizada plana vibrando en la dirección vertical. Eso significa que el vector de Stokes ha de pasar de (1,0,0,0) a (1,-1,0,0); y por cierto, a partir de ahora haremos I=1 para simplificar.
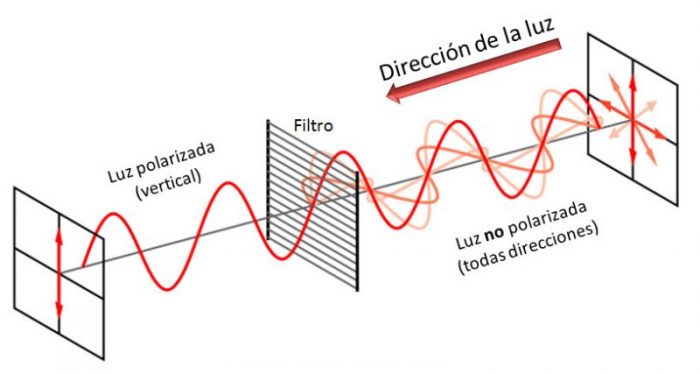
[Original: no recuerdo, pero parece una modificación de esta imagen de la Wikipedia]
Bien, ¿qué matriz nos pasa de un vector a otro? Pues esta:
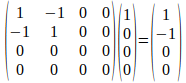
Si queremos que el polarizador tenga un eje de transmisión formando un ángulo cualquiera (digamos θ) con la dirección horizontal, la matriz de Müller del polarizador vendrá dada por:
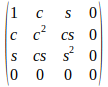
donde s=sen(θ), c=cos(θ) (en el ejemplo anterior, s=0, c=-1). ¿Qué tipo de luz tendremos en ese caso? Veámoslo:
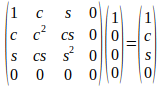
Según lo que valgan c y s, la luz dispersa será polarizada de un tipo u otro. Una cosa interesante es que la V de esa luz siempre será cero, es decir, un polarizador nunca dotar a la luz natural de polarización circular. Para ello disponemos de otros instrumentos, que no voy a describir aquí.
Una cosa importante es que el orden de los factores importa, y mucho, en el cálculo de matrices, y por eso es necesario hacer las cosas con cuidado. Digamos que voy a utilizar dos dispositivos para variar la polarización de la luz. Si uso solamente el dispositivo A, la luz originariamente en estado Ii pasará al estado Is=A*Ii. Si uso el dispositivo B, tres cuartos de lo mismo: As=B*Ii. Ahora bien, si uso primero el A y luego el B, es decir, si la luz encuentra primero el dispositivo A y luego el B, su vector de Stokes pasará de ser Ii a A*Ii, y después a B*A*Ii.
Si cambio el orden de los dispositivos (primero la luz topa con el B y luego con el A), su vector de Stokes pasará de Ii a B*Ii, y luego a B*A*Ii. Y puesto que los productos de matrices A*B y B*A no son idénticos (creedme, ¡ojalá lo fuesen!) ambas situaciones os darán luz dispersa diferente.
Soy consciente de que esto resulta chocante después de haberos pasado la vida oyendo eso de “el orden de los factores no altera el producto”, pero ha llegado el momento de desvelar la sucia verdad: OS HAN ENGAÑADO. Bueno, no del todo. Digamos que eso vale para la multiplicación de ciertas cantidades, como los escalares (hacer 2*4,5 es lo mismo que 4,5*2), y también vale para el llamado producto escalar. Pero no, repito NO sirve para el producto de matrices.
Advertidos quedáis.
Ahora volvamos al asunto que nos interesa: la dispersión de luz por partículas.
Si suponemos que no hay dispersión múltiple (es decir, que la luz dispersada por una partícula no va a re-dispersarse por otra partícula) podemos calcular la dispersión debida a un conjunto de N partículas como la suma de las dispersiones de cada partícula por separado. O dicho en lenguaje matricial, M(total)=M(partícula 1) + M(partícula 2) + … + M (partícula N).
Supongamos para simplificar que todas las partículas son iguales. En ese caso M(total)=N*M(partícula). Eso significa que calculamos la matriz de Müller de la partícula, y con eso ya hemos cumplido. Vale, en la práctica no es tan sencillo, pero aun así ese es el punto de partida.
Ahora toda responder a la pregunta del millón: ¿cómo se hace eso? En el nivel más básico se toman las ecuaciones de Maxwell del electromagnetismo y se resuelven. Pero eso es de todo menos sencillo, y libro tras libro se dedican a resolverla para casos más o menos sencillos. Ahí es donde tengo yo mi campo de actuación.
En cualquier caso, esa matriz de Müller dependerá de dos grandes tipos de factores. Uno de esos tipos es, sencillamente, la dirección de la luz incidente y la de la luz dispersada. En el ejemplo de los polarizadores hemos supuesto implícitamente que la luz no se desviaba de dirección, pero en general ese no será el caso. No importa, esa es la parte sencilla.
La parte complicada viene dada por el otro tipo de factores, los correspondientes a la partícula. Eso lo veremos el próximo día, que tampoco tenemos prisa.
Resumen para dummies. Cuando un sistema cambia el estado de un haz de luz, lo que ha hecho se describe matemáticamente mediante la llamada matriz de Müller del sistema. Podemos obtener la matriz de un conjunto de partículas a partir de la matriz correspondiente a una sola partículas. Esa matriz dependerá de las direcciones de la luz (incidente y dispersa), y también de las propiedades ópticas de la propia partícula.
[Etiquetas: scattering 101]
Deja una respuesta