
Según sea la partícula, así será su matriz de Müller. Los principales parámetros de la partícula que resultan aquí relevantes son tres: tamaño, forma y composición.
El tamaño viene dado por algún parámetro que represente a la partícula. Si fuese esférica nos bastaría con su radio, pero como rara vez es la naturaleza tan sencilla hemos de echar mano de parámetros equivalentes. Por ejemplo, podemos tomar el radio de una esfera que tuviese el mismo volumen V que nuestra partícula. En ese caso hacemos V=(4/3)πr3, así que nuestro radio de volumen equivalente será r=[4/(3πV)]1/3. Un debate interesante en mi campo es si resulta preferible tomar el radio de la esfera de superficie equivalente. También se pueden echar mano de otros parámetros como la longitud mayor de la partícula, o algún parámetro conocido si tiene cierto grado de simetría: la longitud en un cilindro, el eje mayor en un esferoide. Tenemos cierto grado de libertad a la hora de elegir el parámetro de tamaño.
Cualquiera que sea nuestra elección, en muchos, pero que muchos casos, lo importante es el tamaño en relación con la longitud de onda. Una partícula no será “muy grande” o “muy pequeña” en términos absolutos, de modo que un glóbulo rojo será grande para la luz ultravioleta y pequeño para las ondas de radio. Por eso se suele usar una cantidad adimensional llamada parámetro de tamaño. Si el tamaño de la partícula (comoquiera que lo definamos) es r, el parámetro de tamaño será el producto 2πr/λ ¿Por qué? Porque, si recordáis del artículo anterior, esa cantidad es igual a kr, y ese producto aparece en un montón de sitios; recordad la onda plana, por ejemplo, donde E=Eo*sen[kx – ωt+φ]. Así pues, el parámetro de tamaño x=kr nos dice lo grande o pequeña que es la partícula en relación a la onda que incide sobre ellas [OJOCUIDAO: ese “x” no es la “x” que designa el eje horizontal. Ojalá pudiese cambiarle la notación, pero se usa mucho y yo soy un mandado). Por cierto, a ese k=2π/λ se le suele llamar número de onda.
Segunda parte: la forma. Cuando la forma es conocida resulta bastante fácil. Por ejemplo, puedes caracterizar un cilindro de radio r y longitud L mediante el cociente r/L (o el L/r, lo que quieras). Pero si la partícula tiene forma irregular, es todo un engorro. Lo que se suele hacer es aproximarla por una partícula de forma conocida: un prisma, un cilindro, un esferoide, una partícula de Chebyshev. Los métodos más sofisticados tienen en cuenta la forma irregular y la modelan (por ejemplo, mediante un conjunto de dipolos eléctricos) pero eso ya es para nota, y luego tienes el problema de que, en muchos casos, no conoces la forma exacta de la partícula, así que al final acaban aproximando igual.
Tercera parte: la composición. Vamos a usar el índice de refracción, que seguro habéis visto en el colegio. Es el que relacionaba el ángulo de incidencia con el de refracción. Lo llamábais n, y se definía como el cociente entre la velocidad de la luz en el vacío y en ese medio, n=c/v. Por ejemplo, en el agua n es igual a 1,33 porque la luz viaja allí a unos 225.000 km/s.
Ese índice de refracción n es una cantidad real. El problema es que, cuando veíamos la ley de la refracción o la de la reflexión, estábamos simplificando en exceso. Hay dos detalles a tener en cuenta. Uno es que los medios no son transparentes. Incluso el agua pura o el más bello de los cristales absorben algo de la luz cuando ésta a su través. Eso significa que hay que tener en cuenta esa absorción, o si no que se lo digan a los peces de las profundidades abisales.

Eso significa que el índice de refracción tiene que ampliarse para considerar la posibilidad de absorción por el medio. Puede conseguirse haciendo que el índice de refracción sea complejo. Suele usarse el índice de refracción complejo m=n+ik, donde esa k NO es el número de onda k=2π/λ que hemos visto antes. Nuevamente la nomenclatura es bastante rara, pero esto es lo que hay. En cualquier caso, la adopción del índice de refracción complejo m permite incluir el efecto de absorción de las ondas; cuando no exista absorción haremos k=0 y listo.
Segundo detalle a tener en cuenta: lo llamemos n o m, el índice de refracción suele depender de la longitud de onda. En ese caso se dice que el medio es dispersivo. Y aquí tenemos otra confusión de términos, porque en su momento dije que “dispersión” es la forma en que traducimos el “scattering” anglosajón. Espero que no os confundáis. Por mi parte, cuando haya una dependencia n(λ) hablaré de medio dispersivo.
En la siguiente imagen podéis comprobar cómo cambia n con λ para la luz visible . Aparecen cuatro curvas para diferentes temperaturas, pero la dependencia gorda está con la longitud de onda. La variación es de menos de un 1% así que en primera aproximación podemos suponer n constante a la hora de calcular.
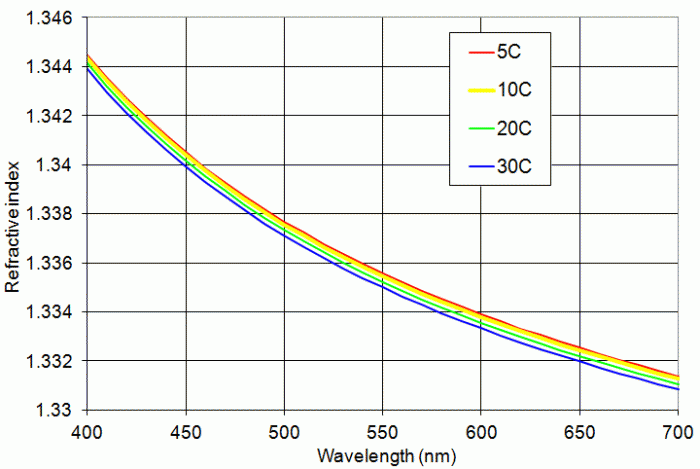
Si la luz fuese un medio no dispersivo, los arcoíris no existirían y en su lugar tendríamos una aburrida franja blanquecina en el cielo, pero como sí es dispersivo la luz del sol se separa en multittud de colores. Cada longitud de onda se desviará de forma distinta, y por eso nos quedamos con la boca abierta frente a esos bonitos arcos de colores que decoran el cielo cuando ha llovido.

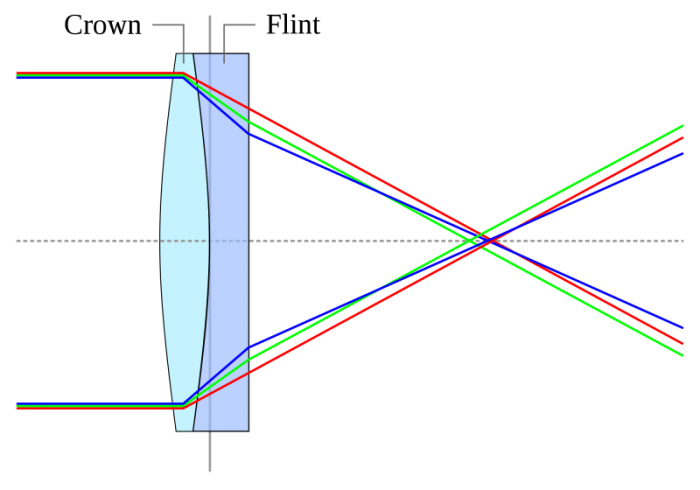
Los fotógrafos saben que, cuando un haz de luz entra en una lente, se dispersará en colores, lo que hará que las fotos tengan tonos irisados. Para evitarlo los objetivos fotográficos constan de dos o más lentes, fabricadas con materiales distintos, de forma que lo que dispersa una lente lo des-dispersa (toma palabro) la otra. El resultado no es perfecto pero es mucho mejor que nada.
El problema viene con k, la parte imaginaria del índice de refracción (m=n+ik). Ese término puede variar salvajemente con la longitud de onda. Para que lo veáis, la siguiente gráfica indica los valores de n (azul) y k (rojo) para ondas que van del ultravioleta lejano (10 nm) hasta ondas de radio (10 m). Es una gráfica semilogarítmica, donde el eje horizontal no varía según la progresión 1,2,3,4… sino 10, 100, 1000…
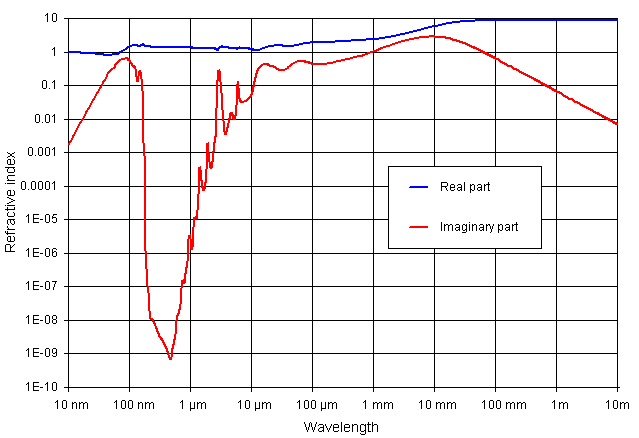
En la región del visible es donde la curva roja está más baja, lo que significa que k es muy pequeño (del orden de la milmillonésima) y por tanto el agua es muy transparente ahí. Es movernos un poco hacia el infrarrojo o el ultravioleta y de repente el agua se convierte en un material absorbente. Un pez dotado de ojos en el ultravioleta vería menos que un gato de escayola.
El hecho de que un medio (sea un bloque como una piscina de agua o un conjunto de partículas como gotas) sea dispersivo es a menudo una molestia a la hora de calcular cantidades. Por otro lado, permite obtener más información del sistema estudiado, ya que podemos medir las “huellas” a distintas longitudes de ondas y extraer más información que si el sistema tuviese un índice de refracción constante. Es lo que se llama medición multiespectral, donde “multiespectral” significa medir a muchas longitudes de onda.
En todo lo anterior supondremos que no se da el fenómeno de anisotropía. En un material anisótropo, el índice de refracción depende de la dirección de donde proviene el haz de luz. Es algo así como el jamón, que tiene vetas y no es lo mismo cortar en una dirección que en otra. Digo lo mismo que siempre: esos materiales son muy interesantes de estudiar, pero no voy a hacerlo aquí.
Lo que sí hay que tener en cuenta es que, en ocasiones, las partículas pueden estar estratificadas. Es decir, puedo tener una esfera con un núcleo de un material y un recubrimiento de otro. Lo habitual en esos casos es resolver el problema homogéneo (por ejemplo, partícula esférica) y luego extender la solución al caso de dos o varias capas.
Un último detalle a tener en cuenta. Resulta que la naturaleza es perversa y raramente las partículas de un sistema son todas iguales en forma o tamaño. Eso comporta problemas computacionales, pero el esquema es el mismo. Es decir, primero resuelvo para una partícula (digamos una esfera) y luego calculo para partículas de varios tamaños. Se suele usar una función de distribución para indicar los tamaños de las partículas del sistema, pero eso lo hablaremos en su momento.
A partir de aquí, toca calcular, lo que significa tomar una partícula de tamaño, forma y composición determinados y darle caña. Habitualmente eso pasa por aplicar las ecuaciones de Maxwell con condiciones de contorno y otros tecnicismos raros. Pero antes de eso veremos casos más sencillos. Hasta la próxima.
Resumen para dummies. A efectos ópticos, las propiedades que definen partícula son forma, tamaño y composición. En ese último caso hay que introducir una cantidad extra para describir la atenuación de un haz de luz cuando atraviesa un medio material. Por lo general los medios son dispersivos, esto es, lo que hacen con la luz depende de la longitud de onda de ésta.
[Etiquetas: scattering 101]
gran aporte. gracias!!