
Siempre se ríen de los científicos porque hacen muchas aproximaciones, y de forma inevitable sale a relucir la vaca esférica en el vacío. Pues sí, somos amantes de las aproximaciones. Nos facilita mucho el trabajo, y también a vosotros. Primero resolvemos el problema en la forma más simplficada posible y luego vamos añadiendo complicaciones.
Es como escoger un coche. Tú no te levantas por la mañana pensando “sí, voy a necesitar un coche y ha de ser el Ford Veleta 1.2 Diesel Forges Edition” Lo primero que haces es pensar qué características ha de tener. No, lo primero es ver si tienes dónde aparcarlo, y sobre todo, si te va a alcanzar el precio. Te pones a pensar si quieres diésel o gasolina, qué diablos es eso del SUV, hasta qué punto trae cuenta un 4×4 en lugar de un monovolumen, qué potencia es la adecuada, qué accesorios deseas, si necesitas financiación… y luego te das cuenta de que se te sale de presupuesto, así que vuelta a evaluar todas las variables.
Algo así tenemos aquí. Vamos a estudiar la dispersión de la luz por partículas, así que comencemos por los casos más sencillos. El problema fundamental es que, cuando la longitud de la onda de luz es comparable al tamaño de las partículas que se encuentra, las interacciones son complejas y hay que dejarse allí el cerebro. ¿Pero y si no es así? ¿Y si la partícula es muy pequeña, o muy grande? Ah, amigo, entonces la cosa se hace mucho más fácil.
Vamos al caso de partícula muy pequeña, es decir, kd<<1, donde k era el número de onda de la luz (está bien, lo habéis olvidado, venga un recordatorio: k=2πλ) y d es algún tamaño característico de la partícula. En esas circunstancias hablamos de dispersión de Rayleigh.
En los libros que manejo, lo habitual es partir de las ecuaciones para dispersión en partículas esféricas y tomar el caso límite de radio tendente a cero. Prefiero hacerlo a la antigua usanza, tal y como el propio Rayleigh las dedujo. El método que usó es el que hoy llamamos análisis dimensional, y me encanta por su elegancia así que aquí va.
Ah, no, que no os he explicado lo que es el análisis dimensional. Básicamente viene a ser eso de no sumar peras y manzanas. Si tenemos una ecuación del tipo A+B+C=D, todas esas cantidades han de pertenecer a la misma magnitud, sea cual sea. No podemos sumar si A es velocidad, B es masa y C energía, ya que no tiene sentido comparar cantidades de magnitudes distintas. Una longitud de un metro es mayor que la de 54 centímetros, pero preguntar si un kilogramo es mayor que un minuto carece de sentido.
Vamos a dejar de lado el vector de Stokes por un momento y centrarnos en la intensidad de luz. Bien, pues nuestro amigo Rayleigh pensó en la dispersión de luz por partículas muy pequeñas. Su idea es que, en ese proceso de dispersión, el campo eléctrico incidente y el disperso se pueden relacionar como Es=A*Ei; donde “A” será una cantidad adimensional, es decir, un número sin más.
En este punto, el análisis dimensional te dice que pienses en qué factores pueden influir en A, es decir ¿de qué parámetros depende A? Rayleigh dijo que, en primer lugar, podría depender del volumen V de la partícula. También puede influir la distancia d de la partícula al punto donde observamos; la longitud de onda λ; la velocidad v con que se propaga la onda; las densidades del éter antes y después de la dispersión (sean D, D’); y otras cantidades que, siendo adimensionales, no podemos determinar mediante análisis dimensional.
En primer lugar, ¿qué es eso de “la densidad del éter”? En aquella época (hablamos de 1871) se creía que había un material impalpable y sutil llamado éter, que se creía necesario para explicar la propagación de ondas electromagnéticas. Ahora sabemos que ese éter no existe, y esa “densidad del éter” se correspondería con la cantidad que llamamos función dieléctrica.
Partimos, pues de algo del tipo A=f(V, d, λ,v, D, D’), es decir, que A es una función de esas seis variables.
Rayleigh decía que la densidad del éter dependía de la masa. Puesto que ninguna otra variable de las mencionadas depende de la masa, la única posibilidad es que A dependa del cociente adimensional D/D’. Cómo lo hace es algo que no podemos precisar, pero sigamos adelante.
Nos queda entonces A=f(V, d, λ,v)
A no puede depender de la velocidad de la luz. ¿Por qué? Pues porque v es la única cantidad que depende del tiempo, y como A no depende de la variable tiempo no puede haber dependencia con v. Vale, estrictamente sí podría haber dependencia entre la velocidad de la luz en el vacío (c) y en la partícula (v), en forma de cociente c/v. Ese cociente es el índice de refracción real n. En efecto, ahora sabemos que A depende de n; más aún, depende del índice de refracción complejo m. Aun así, bien por Rayleigh.
Hemos llegado a A=f(V, d, λ). Vamos a asumir, como hizo Rayleigh, que A depende directamente de V; es decir, a mayor volumen de la partícula mayor campo eléctrico disperso. Eso no sucede siempre pero tiene sentido para partículas muy pequeñas, donde se puede suponer que las moléculas que producen la dispersión en la partícula original ondas con la misma fase. Vamos, que no hay interferencias entre ellas.
Estamos ahora como A=V*f(d, λ)
Se puede aplicar la ley de conservación de la energía para demostrar que el campo eléctrico dispersado depende de la distancia como “algo”/d. Para entenderlo pensad en toda la luz dispersa. Se trata de una cantidad constante pero que se va dispersando cada vez más conforme se aleje de la partícula. A una distancia d su energía se ha repartido por una superficie esférica de radio d, y como el radio de la esfera es proporcional a d2 su intensidad debe disisminuir como 1/d2. Es el mismo argumento que explica por qué una linterna ilumina cada vez menos a distancias crecientes: el haz se extiende por el espacio así que la luz decrece en intensidad. Y puesto que esa intensidad es proporcional al campo eléctrico, si la intensidad va como 1/d2 entonces el campo eléctrico decae como 1/d.
Hemos llegado a la expresión A=V*f(λ)/d
Digamos que f es una expresión del tipo C*λa, donde C es una constante adimensional. Como las dimensiones de V y d son L3 y L, respectivamente, eso significa que la ecuación de dimensiones nos da: L3*L-1*La=L0, lo que significa que A depende inversamente del cuadrado de la longitud de onda: A = Cosas/λ2
Y recordemos que A es la relación entre el campo eléctrico incidente y el disperso. Hemos concluido que el campo disperso decrece con el cuadrado inverso de la longitud de onda. Ahora bien, la intensidad del haz de luz es proporcional al cuadrado del campo. Eso significa que, en general, Id=Cosas/λ2.
Recopilando lo que hemos deducido hasta ahora, la intensidad de la luz dispersa en una dirección determinada por una partícula pequeña es del tipo:
Id = Cosas * V2/(d2*λ4)
Ese “cosas” incluye variables como el índice de refracción de la partícula y la dirección del haz de luz saliente, y no podemos saberlo con tan sólo el análisis dimensional. Aun así hay mucha información interesante:
– La dependencia con el cuadrado de la distancia d2 es algo conocido y sucede siempre que un haz de ondas electromagnéticas se esparce por el espacio. No es nuevo pero está bien que los planes salgan bien
– Lo de la dependencia con el cuadrado deo volumen de la partícula resulta novedoso, y nos dice cuál es la influencia del tamaño de la partícula. Fijaos que si dividiésemos una esfera en N fragmentos iguales, cada fragmento tendría un volumen V/N, con lo que dispersaría una luz que sería (V/N)2 veces menos intensa. Los N fragmentos dispersarían una luz igual a
Id = Cosas * N * (V/N)2/(d2*λ4) = Cosas * (V2 /N)/(d2*λ4)
Es decir, la luz dispersa es N veces menos que la que había antes. Eso quiere decir que, cuanto más finamente dividamos una partícula pequeña, menos luz dispersará. Interesante.
Pero lo mejor viene de la dependencia 1/λ4. Ese “cosas” es aproximadamente constante si el índice de refracción es constante, es decir, si el material es no dispersivo. Ese no suele ser el caso en general, pero podemos suponer que el índice es aproximadamente constante en luz visible. Vamos a suponer que la luz incidente sobre la partícula tiene un 50% de luz roja (longitud de onda 633 nm) y un 50% de luz azul (longitud de onda 488 nm). Si nos ponemos en una dirección y vemos la luz dispersa, veremos que tendrá una intensidad en luz azul de Id(azul) y una de luz roja ID(roja). ¿Seguirá la mezcla azul/rojo al 50%? Pues no. Fijaos. Si divido ambas intensidades de luz dispersa sale esto:
Id(azul)/Id(rojo) = (Cosas/4884) / (Cosas/6334) = (633/488)4 = 2,83
Es decir, la luz dispersa en azul es casi tres veces más intensa que la roja. O dicho de otro modo, el porcentaje 50% azul – 50% rojo que tenía la luz antes de caer sobre la partícula se ha convertido en 26% rojo – 74 % azul. La luz dispersa se ha azulado.
Ahora suponed que la luz es la del sol y las partículas que dispersan su luz son sencillamente las moléculas de aire que hay en la atmósfera. Al mirar al cielo, lo que veis es la luz dispersa, que como hemos visto tienen mayor componente azul que roja.
Acabáis de comprender por qué el cielo es azul.
Ah, y puesto que la luz dispersa tiene mayor componente de azul, la luz que no se ha disperso y sigue su camino tendrá mayor componente de rojo.
Por eso los atardeceres son rojizos.
¿Y por qué la luz violeta, de menor longitud que el azul, no se dispersa más todavía? Es decir, ¿por qué el cielo no es violeta? Resulta que la luz incidente del sol tiene una cantidad similar de luz azul y roja, pero contiene muy poco violeta; así que, aunque la dispersión es mayor en el violeta, contamos con luz incicente muy poco violeta para empezar. Además, parece que nuestros ojos son menos sensibles al violeta que al azul. Lástima, porque un cielo violeta sería una pasada.
¿A que mola la Física?
Sería genial acabar aquí esta entrada, pero no quiero dejarla incompleta. Vamos a terminarla indicando cuál sería la matriz de Müller para un conjunto de N partículas esféricas de radio r. Lo habitual, como dije antes, es tomar la teoría completa para esferas de radio arbitrario y hacer ese radio muy pequeño, lo que nos da pie a hacer aproximaciones. Como no hemos visto esa teoría, mejor paso a dar la fórmula y punto.
Necesitamos indicar la dirección del haz de luz saliente. Para ello usaremos coordenadas esféricas.
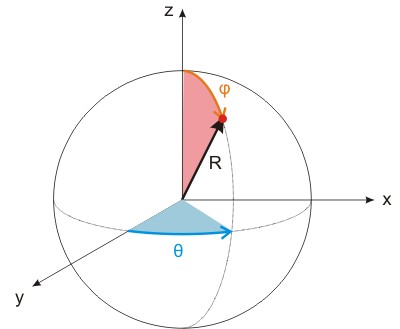
Vamos a suponer que el haz de luz incidente viene de la parte negativa del eje y. La dirección de la luz dispersa, incidada por la flechita negra, estará caracterizado por los ángulos (θ,φ). Bien, pues resulta que la matriz de Müller viene dada por la siguiente expresión:
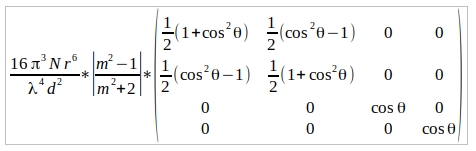
Podéis jugar con los vectores de Stokes y comprobaréis por ejemplo que un haz de luz natural (no polarizado), al dispersarse, se convierte en parcialmente polarizado.
A partir de aquí se puede ir modificando el conjunto de hipótesis de partida. Por ejemplo, la dispersión de Rayleigh para partículas no esféricas tiene una matriz de Müller levemente distinta (en realidad me cuesta encontrar datos porque todo el mundo adora las esferas pequeñitas, por lo visto). Hay una extensión llamada aproximación de Rayleigh-Gans que permite su uso con partículas más grandes que las de Rayleigh, bajo la condición de que el material que las forme sea casi transparente: |m-1|<<1.
Y aquí lo dejamos. En el próximo episodio veremos qué pasa con partículas muy gordas, y os enseñaré cómo se hace un arcoíris.
Resumen para dummies. Cuando las partículas responsables de la dispersión de luz son mucho más pequeñas que la longitud de onda incidente, la llamada aproximación de Rayleigh permite un análisis sencillo del caso. La luz dispersa tiene una componente de ondas cortas (luz azul) más fuerte que la de ondas largas (luz roja), motivo por el cual el cielo es azul.
[Etiquetas: scattering 101]
Deja una respuesta