
Hemos visto cómo dispersa la luz una partícula muy pequeña. Ahora nos vamos al otro extremo.
Cuando un objeto es mucho, mucho mayor que su longitud de onda estamos en lo que se denomina óptica geométrica. Eso quiere decir que podemos tratar la luz como rayos compuestos por partículas llamadas fotones; bueno, como rayos y punto, no hace falta detallar lo que hay en el interior.
La óptica geométrica fue impulsada por Isaac Newton. A pesar de que había experimentos que la contradecían, como la interferencia o la polarización, Newton se mantuvo en sus trece; en aquella época regía los destinos de la física europea con mano de hierro y, reconozcámoslo, cuando quería se comportaba como un cachocabrón de esos que no quieres encontrarte en un callejón oscuro (sus guerras con Leibnitz sobre la invención del cálculo integral son legendarias). A pesar de ello se fue imponiendo la concepción de la luz como ondas, lo que dio lugar a la llamada óptica física. Por cierto que odio ese término, porque da a entende que la otra, la geométrica, no es física, y tan física es una como otra.
En cualquier caso, podemos aplicar óptica geométrica como primera aproximación cuando la partícula es muy grande. El motivo es que, si eres mucho más grandote que la longitud de la onda, no puedes notar que la luz son ondas.
Vamos a ilustrar lo que sigue usando una partícula esférica (para otra geometría de partícula la situación será más difícil de analizar). Digamos que tenemos una esfera opaca, de modo que la luz no puede entrar. En ese caso sería como un espejo esférico, y podríamos examinar la luz saliente sin más que aplicar la habitual ley de la reflexión: ángulo de incidencia igual a ángulo de reflexión.
Nada de particular. Pero ahora supongamos que la luz pueden entrar en la partícula (porque sea transparente, por ejemplo). En ese caso las cosas se ponen interesantes. Cuando el haz de luz choca contra la superficie de la partícula, parte del haz se refleja y parte penetra en el interior. La parte que entra ha cambiado de dirección, que podemos conocer mediante la ley de Snell de la refracción. Ya sabéis, eso de ni*sen(θi)=nt*sen(θt). Si el haz de luz viene del aire, ni es aproximadamente igual a 1, nt es el índice de refracción de la partícula, y los ángulos son los formados por los haces de luz (incidente y refractado) con la dirección perpendicular a la superficie.
Bueno, vale, aquí va un dibujito:
[Fuente original: libro “Absorption and Scattering of Light by Small Particles” de Craig F. Bohren y Donald R. Huffman, imagen 7.1, página 167]
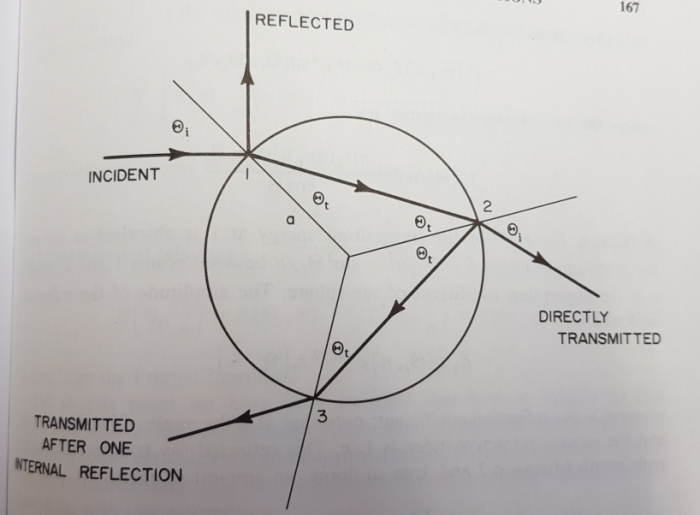
En la imagen el haz de luz entrante (incident) entra en el punto 1, se desvía y acaba tocando de nuevo la superficie en el punto 2. Nuevamente el haz de luz se divide en dos partes, una que sale de la partícula (directly transmitted) y otra que se refleja. La luz puede seguir este proceso varias veces, como el haz que sale en el punto 3 (transmitted after one internal reflection).
¿Cuántas veces puede un haz de luz rebotar en la partícula? Muchas, pero tened en cuenta una cosa: cada vez que toca la superficie (en los puntos 1, 2, 3…) el haz rebotado pierde energía, en parte porque el rayo saliente tiene energía, en parte porque el material suele ser más o menos absorbente. Eso significa que tendremos rayos de luz salientes en direcciones concretas. Pero claro, esas direcciones dependerán de la dirección de entrada, que a su vez depende del punto en el que el haz de luz toca la partícula. El resultado es un jaleo.
Pero podemos simplificar. Se puede ver en qué direcciones la intensidad de luz saliente es máxima. Vamos a suponer que el ángulo θ=0 representa la dirección de la luz incidente, de modo que θ=180º sería luz que volviese en sentido opuesto. Vamos a suponer un índice de refracción para la partícula de n=1,33. Bien, haciendo algunos cálculos (que os voy a ahorrar), sale lo siguiente:
– En primer lugar, el haz de luz que se refleja sin entrar en la partícula (reflected) sale rebotado y se lleva el 6,6% de la energía dispersa por la partículas
– El haz de luz “directly transmitted” desaparece
– El primer haz saliente que puede verse es el que ha sufrido una sola reflexión interna; en la figura es el que sale por el punto 3, el “transmitted after one internal reflection”. Su ángulo de salida es de θ=138º, es decir, casi rebota hacia atrás, y ese haz lleva el 88% de la luz dispersada por la partícula.
– El siguiente haz saliente es el que sufre dos reflexiones internas (no aparece en el dibujo), saldrá a un ángulo θ=129º, y será responsable del 4% de la luz dispersa.
– El tercer haz saliente… bueno, podríamos seguir así, pero no tiene sentido. Este tercer haz saliente tiene una intensidad que es el 0,6% de la luz dispersa; el cuarto lleva el 0,17% de luz dispersa, y así sucesivamente.
Bien, ahora vamos a ver cómo se ve eso.
Digamos que nuestra partícula se encuentra en el centro de una circunferencia imaginaria. La luz entra en la partícula y luego sale, y la dirección que tome define el ángulo de salida. Pues bien, cuando el observador se ponga en algunos de los ángulos que se han mencionado antes, verá un destello de luz más brillante, algo así:
Como vimos antes, para el ángulo 138º la intensidad de luz dispersa es máxima, luego hay un segundo ángulo de dispersión con luz brillante (pero menos) a 129º, y después hay otros que no vamos a poner aquí porque su intensidad es muy baja.
Eso en el plano que indica la figura. ¿Y si estuviese por encima de ese plano? Pues lo mismo. Lo único que importa aquí es que el ángulo de desviación sea alguno de esos dos.
Bien, ahora supongamos que esas bolitas esféricas son de agua. De hecho, no es casualidad haber escogido el índice de refracción sea 1,33 ya que es aproximadamente el del agua. Vale, pues tenemos gotitas de agua en la atmósfera, muchas de ellas. Cada partícula definirá un plano distinto con la luz incidente y la dispersa, y el resultado es que, al mirar al cielo, no veremos un punto brillante a 138º y otro a 129º, sino que ahora son bandas, es decir, circunferencias de más o menos grosor. Lo que veríamos sería un anillo brillante de color blanco, otro anillo más débil circunscribiendo al anterior…
Pero eso NO es lo que vemos tras un día lluvioso. Y el motivo es que el agua no tiene el mismo índice de refracción para todas las longitudes de onda. Como vimos en la entrada “Propiedades particulares”, el índice de refracción en el agua varía entre 1,331 y 1,345 en el visible. Eso significa que el haz de luz entrante se divide en haces de colores, y al salir de la partícula cada uno de esos colores tomará una dirección distinta. La diferencia es sutil pero de una gran belleza.
La banda de aburrida luz blanca se ha convertido en un maravilloso arcoíris. Y, si la visibilidad es buena, tendremos un doble arcoíris. Valga como ejemplo este hermoso arcoíris que pudimos disfrutar en Granada el 31 de marzo de 2013:

Como véis, también tenemos zonas brillantes (dentro del arcoíris principal) y oscuras (entre ambos arcoíris), pero en lo fundamental tenemos lo que os dije: dispersión de la luz en partículas esféricas grandes.
¿Cuántos arcoíris pueden verse? Como he dicho, si tenemos suerte y hay buena visibilidad podemos ver dos (que, por cierto, tienen el orden de los colores invertidos, fijaos). Con mucha suerte, tres. No sé cuántos pueden verse o dónde está el récord en esto, pero en el laboratorio se pueden hacer virguerías con los arcoíris. O eso dicen.
Bien, ahora vamos para nota. Tampoco es que haga falta, pero ya puestos…
Resulta que las gotitas de agua en suspensión aérea no son exactamente esféricas. El peso tiende a hacer que caen, y el aire las deforma un poco. El resultado es algo similar a lo que hemos visto, con pequeñas diferencias. Mi compañero bloguero de Naukas Francis Villatoro tiene, por si os interesan, datos de simulaciones por ordenador aquí.
Por cierto, hoy no he hablado de vectores de Stokes, de matrices de Müller, de polarización ni nada de eso. Bueno, también puede hacerse, pero prefiero dejaros con el buen sabor de boca de un hermoso arcoíris. El siguiente paso será estudiar partículas esféricas ni muy pequeñas ni muy grandes, y ahí sí haremos uso de esa parafernalia que os comenté en entradas anteriores. Tranquilos, no va a doler.
Resumen para dummies. La dispersión de la luz por una partícula esférica grande puede calcularse de modo sencillo desde la aproximación de óptica geométrica. Así podemos explicar, por ejemplo, esas bandas circulares de luz que aparecen en el cielo cuando ha llovido, y que gracias al carácter dispersivo del agua se nos muestra como brillantes arcoíris de colores.
[Etiquetas: scattering 101]
Deja una respuesta