Huellas de luz (7): las vacas esféricas de Gustav Mie

Bien, ha llegado la hora de ponernos serios. A partir de ahora nada de simplificaciones tipo partículas muy pequeñas, o muy grandes. Vamos a ver cómo dispersan luz las partículas esféricas del tamaño que sea.

La resolución de este problema está ligado al nombre de Gustav Mie, quien en 1908 publicó un artículo describiendo lo que hoy conocemos por “teoría de Mie” y que describe la dispersión de luz por partículas esféricas. Cien años largos y todavía la estamos usando, fundamentalmente porque es mucho más sencilla (relativamente hablando, claro) que otras teorías para partículas no esféricas, y es un buen punto de partida para tratar problemas de dispersión de luz. Recuerdo que incluso traduje el artículo original del alemán (oh, divina juventud), lo que me dio acceso directo a esta teoría y al modo de trabajar de Mie. Usaré tanto el original de Mie como otros trabajos clásicos como el libro de Bohren-Huffman, que ya usé en otras entradas anteriores.

Por cierto, Mie se pronuncia “mi”, no “mai”, porque es un apellido alemán. Vale, empezamos.

Mie quería explicar el color de algunas suspensiones de oro en estado coloidal (en el que las partículas son muy pequeñas pero no tanto que lleguen al tamaño atómico). El punto de partida lara la explicación son las ecuaciones de Maxwell del campo electromagnético. Y resolver esas ecuaciones son palabras mayores.

¿Por qué? Pues porque no son las típicas ecuaciones dondo conoces algunas variables y despejas las que te faltan. Por ejemplo, la ecuación para el período T de un péndulo simple de longitud L es T = 2π*raíz(g/L), donde g es la aceleración de la gravedad. En mi laboratorio de prácticas los alumnos miden T y L, lo que les permite obtener g. Fácil y expeditivo.

Las ecuaciones de Maxwell no se pueden “despejar”, no son de esa clase. Os voy a poner un ejemplo. Digamos que en una región del espacio tenemos un campo magnético vectorial B, que tiene tres componentes (B_x, B_y, B_z). Cada componente dependerá del lugar en que nos encontremos, es decir, será función de las coordenadas espaciales. Eso se escribe como B_x(x,y,z), y lo mismo para B_y y B_z. Puesto que B_x es función de x,y,z, eso significa que puedo derivar B_x con relación a x, con relación a y o con relación a z. La derivada de B_x con relación a x se escribe como ∂B_x/∂x (ojo con ese signo de división /, que en este caso NO indica un cociente, es sólo notación).

Vale, pues lo que nos dice una de las ecuaciones de Maxwell es que las componente del vector B tienen que cumplir la siguiente relación:

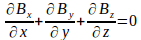
A partir de esa información, ¿podemos saber lo que valen B_x, B_y y B_z? La respuesta estándar es: ¡¡NI DE COÑA!! Es como si Sherlock Holmes buscase al profesor Moriarty y la única información que tuviese de él fuese “bueno, tiene dos piernas, tal vez pasó las paperas y ahora vive en una ciudad cuyo nombre no comienza por R”

Evidentemente hay que currárselo mucho, mucho más para poder llegar a alguna parte. Las ecuaciones de Maxwell, usadas con astucia, pueden resolverse al menos en algunos casos de forma exacta, en otros de forma aproximada.

Mie logró resolverlo de forma exacta. Para ello utilizó coordenadas esféricas, no cartesianes. Es decir, en lugar del tradicional (x,y,z) utilizó otro conjunto de tres coordenadas. Para simplificarlo, os daré un ejemplo: la latitud y longitud, junto con la distancia al centro de la Tierra, forman un sistema de coordenadas esféricas. Hay muchas formas de indicar la posición de un cuerpo, es decir, muchos tipos de sistemas de coordenadas, y resulta que en coordenadas esféricas sí podemos resolver el problema de la dispersión de luz para partículas esféricas.

Vamos, pues, a usar un sistema de tres coordenadas (r,θ,φ), donde para seguir el ejemplo anterior r es la distancia al origen de coordenadas, θ es la longitud y φ es la latitud. Algo así:

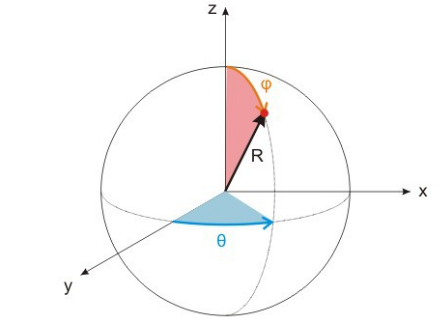
ACLARACIONES MENORES PERO IMPORTANTES:

– En realidad, esa φ que aparece en la figura es la co-latitud, es decir, 90º-latitud, pero ese detalle no importa en lo que sigue.

– Se supone que el haz de luz incidente viene por la parte negativa del eje z y sale dispersa en la dirección indicada por el vector R.

– Habitualmente la dispersión de Mie usa un sistema de coordenadas levemente distinto, en el que los ángulos θ y φ están intercambiados respecto al dibujo de arriba. Por lo que puedo ver, se trata de una elección hecha por el propio Gustav Mie en su artículo de 1908, y todos los demás hemos seguido esa notación desde entonces. No importa, con tal que sepamos qué notación estamos usando. Fijaos si importa poco, que después de tantos años trabajando en el tema me doy cuenta AHORA, al escribir este párrafo, del cambio de notación.

Voy a simplificar mucho porque tampoco es cosa de aburrir sin necesidad (cuando yo aburro, siempre hay una necesidad). Comenzaremos yéndonos a una región del espacio compuesta por un medio homogéneo e isótropo; esto es, que tiene las mismas propiedades dentro de esa región, y donde no hay una dirección privilegiada. Nuestro objetivo es obtener una función que denotaremos ψ, que es un escalar (no un vector) y que llamaremos “función escalar de ondas” (IMPORTANTE: a pesar de la similitud, NO tiene nada que ver con la función de onda que se usa en mecánica cuántica).

Lo bueno de esa función ψ es que, haciéndole algunas perrerías (bueno, derivándola y tal pascual) podemos obtener los vectores del campo eléctrico E y de campo magnético B, así que resolver el problema que nos ocupa pasa por determinar el valor de ψ. Lo que en apariencia no es sencillo, porque las ecuaciones de Maxwell nos dicen que esa función debe cumplir con esta ecuación. Tomad aire, chicos:

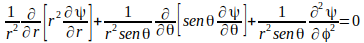
Pero ahora viene lo bueno. Resulta que, en coordenadas esféricas, este problema es separable. Eso significa que puedo escribir la función ψ como producto de otras tres funciones: una que sólo depende de r, otra que sólo depende de θ y una tercera que sólo depende de φ:

Tener una ecuación separable es como que te toque la lotería, así que vamos a cobrar el premio. La consecuencia imnediata de la separación de soluciones es que la ecuación diferencial se nos convierte en tres ecuaciones muy sencillas de resolver. Bueno, mejor diré bastante más sencillas. Vamos a verlos.

Antes, sin embargo, un aviso: realmente no hay una única solución. Es decir, esas tres funciones separables no son tres, sino muchas. No importa con tal que sepamos cuáles són y como se calculan. Para indicar todas esas soluciones utilizaremos dos números naturales: n (=0,1,2…) y m (=-n,-n+1 … n-1,n)

Primero vamos a lo sencillo, la coordenada φ. Las funciones Φ_m son del tipo cos(mφ), sen(mφ). Más sencillo, imposible, ¿verdad? Lástima que lo que sigue se complique algo más. Las soluciones R_n(r) dependen del número entero n y reciben el nombre de funciones esféricas de Bessel. No son facilonas de manejar pero se pueden calcular, y el proceso de cálculo es interesante, tanto que lo comentaremos más en profundidad, pero lo dejaremos para otro día. Finalmente, las funciones Θ_m,n suelen escribirse como P_n^m y se llaman polinomios asociados de Legendre.

Vale, ahora vamos a hacer una pausa y recapitular. Lo que hemos hecho es describir los campos eléctricos y magnéticos en una región del espacio homogénea, y ponerlos como combinación de funciones que podemos calcular (esos polinomios asociados de Legendre, las funciones esféricas de Bessel, y por supuesto los senos y cosenos). Pero eso de estar en “una región homogénea” es muy aburrido. Nosotros lo que queremos es estudiar dispersión de luz por partículas, y eso esencialmente consiste en hacer pasar nuestros campos eléctrico y magnético por regiones del espacio que no son homogéneas. Vamos, que pasar del vacío a una gota de agua no es muy homogéneo que digamos. ¿Cómo resolvemos ese problema?

Bien, la idea pasa por resolver la función de onda en el medio que hay por fuera de la partícula, hacer otro tanto en el medio interior (esa es nuestra vaca esférica), y finalmente relacionar ambas funciones. Ese “finalmente” suele ser de lo más complicado, pero de nuevo el hecho de que todo sea tan bonitamente esférico nos da una relación que nos simplifica el problema.

La relación proviene del hecho siguiente: el campo electromagnético va a su bola dentro de la partícula y también fuera, pero en la superficie de la partícula tiene que cumplir ciertas relaciones que se conocen como condiciones de contorno. El símil sería tener un equipo de construcción de túneles en Francia y otro en España. Cada uno de ellos perfora un túnel en los Pirineos, y resulta que pueden hacerlo como quiera, pero con la condición de que en un punto exacto y a una hora exacta ambos túneles han de unirse. Esa sería su condición de contorno.

En el caso de un túnel real, la “condición de contorno” se hace lo más sencilla posible: los tramos del túnel son rectos, los dos equipos de perforación se encuentran uno frente al otro (aunque con una montaña por delante), y en ese caso no se sabe bien cúando se empalmarán los dos tramos. Se puede hacer una estimación, claro, pero luego todo cambia por mil problemas: fallos de las máquinas, vías de agua, roca más dura de lo previsto… así que los dos presidentes tienen que tener agendas abiertas si es que desean ir a hacerse la foto cuando haya terminado la perforación del túnel.

La dispersión de luz es mucho más exigente que eso. Si te acercas a la superficie de la partícula por un lado (el exterior) y por otro (el interior), tanto el vector de campo eléctrico como el de campo magnético han de llegar a la superficie de forma perpendicular a dicha superficie. Obligatoriamente. De otro modo el fantasma de Maxwell se nos aparece y no querrás verlo enfadado, te lo aseguro.

Lo que sigue es matemáticamente complicado pero realmente es fácil de describir. Básicamente ponemos los campos interior y exterior como combinación de esas funciones que vimos antes (polinomios asociados de Legendre, funciones de Bessel), y a continuación imponemos la condición de contorno a la superficie. Como la partícula es esférica, el resultado es un conjunto de relaciones entre funciones de Bessel dentro y fuera de la partícula; y a partir de ahí podemos obtener la matriz de Müller, de la que os hablé hace algún tiempo y que contiene toda la información relevante sobre la partícula a efectos de dispersar luz.

Ya estamos cerca, así que prosigamos. Sean m_p y m_m los índices de refracción de la partícula y del medio material en que se encuentra (aire, agua, el vacío, lo que sea). La cantidad m=m_p/m_m es el índice de refracción relativo. Si la luz incidente tiene longitud λ, nos inventamos una cantidad llamada número de onda: k=2π/λ. Vamos también a suponer que la partícula no es magnética, o como mínimo que la permeabilidad magnética del medio y la partícula son iguales (así obtendremos más fácilmente una solución).

Ahora un pequeño rincón para la confusión. Siempre hemos usado la letra x para indicar la componente x en un sistema de coordenadas cartesianas. Por desgracia, hay muchas más variables en física que letras disponibles (y mira que hemos echado mano de letras latinas, griegas, hebreas, con subíndices, superíndices, negrilla, cursiva y de todo, pero ni aun así nos basta), así que vamos a usar x para indicar el tamaño de la partícula. Será x=kr=2πr/λ, es decir, la circunferencia de la partícula divididad por la longitud de onda. A veces se le llama parámetro de tamaño.

¿Por qué esa cantidad tan aparentemente rara? Pues porque las condiciones de contorno dependen de esa cantidad, pero no de la longitud de onda o el radio directamente. El propio concepto de grande o pequeño cambia. En una entrada anterior vimos la dispersión de Rayleigh, y dije que era para partículas pequeñas. ¿Pero qué es una partícula pequeña? El tamaño no se mide en relación a nosotros sino a la longitud de la onda que le lancemos. Una bacteria será muy pequeña para una onda de radio pero enorme para los rayos ultravioleta. A partir de ahora, los conceptos de pequeño y grande vienen relacionados con la longitud de onda, y lo calibraremos con el valor de x. ¿Que x vale 0,001? Pues es dispersión de Rayleigh aunque la partícula mida un kilómetro.

Y vamos por fin a lo que nos interesa, que es la matriz de Müller. Las condiciones de contorno nos ayudan. Primero calculamos las siguientes cantidades:

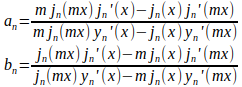
(j_n, y_n son las funciones esféricas de Bessel, y la tilde ‘ indica una derivada). Luego tomamos los polinomios esféricos de Legendre de orden n y grado 1, y definimos las funciones angulares:

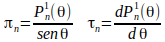
Tercer paso, hacemos las siguientes sumas infinitas:

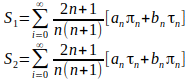
¡Y ya lo tenemos! Porque la matriz de Müller (salvo por una constante de normalización que aquí no importa) es

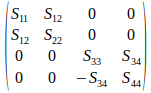
donde, como puede verse, la mitad de los elementos de matriz son cero (básicamente por motivos de simetría), y los seis elementos independientes no nulos son:

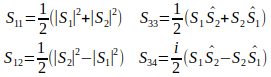
donde |a| indica módulo y el símbolo del sombrerito indica el complejo conjugado (recordemos que tanto S₁ como S₂ son cantidades complejas).

De esa manera, si calculamos esas funciones S₁ y S₂ lo tenemos todo hecho. Y lo mejor de todo es que esas funciones sólo dependen del tamaño de la partícula, de la longitud de onda incidente, de la dirección de salida de la luz y de los índices de refracción de partícula y medio. Ya está. No importa si la luz incidente es una onda plana o no, si está polarizada, si hace el pino con las orejas. Pueden lanzarnos todo tipo de ondas, que ya le tenemos la matriz de Müller lista.

Resumen para dummies. La dispersión de luz para partículas esféricas homogéneas puede obtenerse a partir de las ecuaciones de Maxwell. Para ello hay que calcular diversas funciones como los polinomios asociados de Legendre y las funciones esféricas de Bessel. Solamente hay que conocer la composición de la partícula y del medio, el tamaño de la esfera (relativa a la longitud de onda) y poquito más.