En Física necesitamos la matemática pero en ocasiones los resultados matemáticos no producen resultados físicos, es decir, no respetan las leyes, los modelos de la Física o el espacio físico.
El primer ejemplo son las raíces de un polinomio. Las raíces de un polinomio de grado 2, cuya variable es un tiempo o una distancia, pueden ser reales positivas o negativas o incluso imaginarias conjugadas. Las raíces de polinomio de grado 3 o superior de una magnitud física no oscilatoria pueden ser reales y/o imaginarias conjugadas.
El segundo ejemplo es la interpretación variacional condicionada del Principio de Hamilton para sistemas no holónomos (no integrables)[1,2]. El Teorema Fundamental del Cálculo Variaciones es puramente matemático. Las ecuaciones de Euler-Lagrange para sistemas holónomos sí cumplen ambas perspectivas.
El tercer ejemplo es la Mecánica Jerky. La Mecánica tiene por objetivo predecir la trayectoria de los cuerpos, cuya curvatura local depende a lo sumo de la segunda derivada temporal de las posiciones. La segunda derivada temporal es todo lo que se necesita para diferenciar estados naturales de movimiento. De ahí que sean inconsistentes modelados matemáticos de sistemas físicos clásicos basados en derivadas de la aceleración. Otra cuestión es lo que ocurre con la radiación electromagnética de cargas eléctricas oscilantes, donde existe una fuerza de reacción por radiación o amortiguamiento radiante.
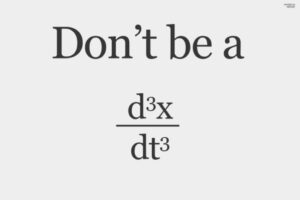
El cuarto ejemplo es la Electrodinámica de Weber (y Phipps)[3] basada en un único potencial escalar, central y dependiente de la celeridad relativa. Este enfoque de la Electrodinámica no describe las ondas electromagnéticas y es incompatible con la Relatividad Especial.
Y el quinto ejemplo es el teorema de Bertrand, para encontrar los potenciales centrales capaces de producir órbitas cerradas. La condición necesaria es matemática pero la suficiente es física. De ahí que sólo los potenciales tipo-culombiano y tipo-Hooke son capaces de ello.
