Supongamos medios materiales no dispersivos. Por el principio de superposición, dos ondas planas viajeras en direcciones de propagación oblicuas se encuentran en un punto donde interfieren. Las ondas longitudinales (ondas de densidad) además de transmitir energía, también transmiten momento lineal (no así las ondas transversales). Sin embargo, las ondas longitudinales tras interferir no intercambian momento lineal y por tanto no colisionan en el sentido corpuscular. Las ondas en general cambian de dirección de propagación cuando atraviesan una frontera entre medios, al cambiar de velocidad de fase.
Resonancia en energía
Decimos que un oscilador armónico amortiguado forzado se mueve en régimen estacionario cuando la potencia (fuerza*velocidad) disipada promedio coincide con la de entrada promedio, sin que esto signifique que la energía mecánica se conserve. Este mismo oscilador entra en resonancia energética cuando su rendimiento es máximo porque fuerza externa y posición actúan en cuadratura de fase: el pico de fuerza coincide con el paso instantáneo por el equilibrio (donde la velocidad es máxima).
Por otro lado, para que el oscilador resuene en amplitud, la fuerza externa y la posición no están en cuadratura de fase. En este caso, la respuesta en amplitud es máxima pero no su rendimiento en potencia.
Fuerzas centrales hermanadas
Las fuerzas centrales atractivas tipo-culombiana (o gravitatorio) y tipo-Hooke tienen estrechos vínculos. Son las únicas fuerzas físicas capaces de generar órbitas cerradas, con las condiciones iniciales apropiadas. Y esas órbitas son elipses, donde uno de sus focos como su centro geométrico coincidirán con los respectivos centros de fuerza. Pero la hermandad entre estas interacciones llega a su culmen cuando se utiliza una transformación de coordenadas y de tiempo sobre el Hamiltoniano del sistema culombiano, para hacerlo separable, y se reproduce la forma del Hamiltoniano elástico. El escalado en tiempo está vinculado al diferente origen de coordenadas de las órbitas elípticas (anomalía excéntrica).
En el problema de Kepler existe el vector Runge-Lenz que es una constante (vectorial) del movimiento mientras que en el oscilador armónico, se define un tensor simétrico con 6 invariantes.
Referencia: https://math.ucr.edu/home/baez/gravitational.html
Rigor matemático vs. rigor mortis
En Física necesitamos la matemática pero en ocasiones los resultados matemáticos no producen resultados físicos, es decir, no respetan las leyes, los modelos de la Física o el espacio físico.
El primer ejemplo son las raíces de un polinomio. Las raíces de un polinomio de grado 2, cuya variable es un tiempo o una distancia, pueden ser reales positivas o negativas o incluso imaginarias conjugadas. Las raíces de polinomio de grado 3 o superior de una magnitud física no oscilatoria pueden ser reales y/o imaginarias conjugadas.
El segundo ejemplo es la interpretación variacional condicionada del Principio de Hamilton para sistemas no holónomos (no integrables)[1,2]. El Teorema Fundamental del Cálculo Variaciones es puramente matemático. Las ecuaciones de Euler-Lagrange para sistemas holónomos sí cumplen ambas perspectivas.
El tercer ejemplo es la Mecánica Jerky. La Mecánica tiene por objetivo predecir la trayectoria de los cuerpos, cuya curvatura local depende a lo sumo de la segunda derivada temporal de las posiciones. La segunda derivada temporal es todo lo que se necesita para diferenciar estados naturales de movimiento. De ahí que sean inconsistentes modelados matemáticos de sistemas físicos basados en derivadas de la aceleración.
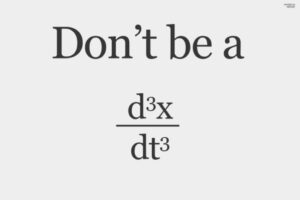
El cuarto ejemplo es la Electrodinámica de Weber (y Phipps)[3] basada en un único potencial escalar, central y dependiente de la celeridad relativa. Este enfoque de la Electrodinámica no describe las ondas electromagnéticas y es incompatible con la Relatividad Especial.
Y el quinto ejemplo es el teorema de Bertrand, para encontrar los potenciales centrales capaces de producir órbitas cerradas. La condición necesaria es matemática pero la suficiente es física. De ahí que sólo los potenciales tipo-culombiano y tipo-Hooke son capaces de ello.
Contribución al movimiento de campos de fuerzas
Un campo de fuerzas puede contribuir al movimiento a través de su capacidad de trasladar cuerpos entre puntos privilegiados (divergencia) y cambiar la orientación de cuerpos alrededor de direcciones axiales privilegiadas (rotacional) [1]. La primera forma de contribuir es a través del desplazamiento (cambios en energía cinética) mientras que la segunda a través del estado de movimiento (cambios en momento angular). La fuerza electrostática (puntos privilegiados pero sin direcciones privilegiadas) contribuye al movimiento de cargas eléctricas por desplazamiento, cambiando su energía cinética sin cambios en su momento angular. La fuerza magnética de Lorentz (sin puntos privilegiados pero direcciones axiales privilegiadas) contribuye al movimiento de cargas eléctricas por cambios en su momento angular, no en su energía cinética. En realidad, esto último se debe a la dependencia con la velocidad en forma de producto vectorial.
Las fuerzas irrotacionales derivan de un potencial escalar que sólo depende de la posición y, si acaso, del tiempo, sólo contribuyen al movimiento por cambios en la energía cinética, es decir, a través de su trabajo mecánico (Teorema de las Fuerzas Vivas). Las fuerzas rotacionales (no necesariamente solenoidales), que derivan de un potencial generalizado, que depende además de la velocidad, también contribuyen al movimiento por cambios en el momento lineal/angular. La fuerza electromagnética es rotacional.
