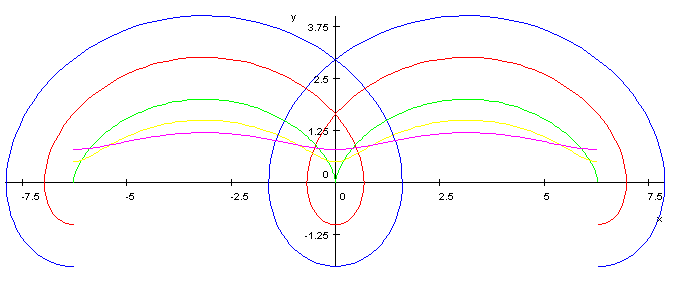
Los campos (potenciales) que dependen con la distancia como 1/r, aunque manifiestan una singularidad en el origen de coordenadas, son integrables en 1D y 2D incluso en dominios cerrados que contengan el origen de coordenadas. Si el espacio se encoge más rápido de lo que el campo crece, la singularidad es débil.
Fuerzas de ligadura en goznes/rodamientos
Cuando en un problema de física o ingeniería existe un eje vertical de rotación con dos goznes/rodamientos, casi siempre asumimos el diseño isostático:
- Las fuerzas de reacción en los goznes no son iguales.
- Se anula deliberadamente una de las reacciones axiales de manera que el otro gozne soporte el 100% del peso.
Para que el sistema sea isostático en la dirección axial (vertical), solo una articulación debe restringir ese movimiento.
En un diseño hiperestático, ambos goznes (el superior y el inferior) están rígidamente fijos al eje e impiden el movimiento axial (vertical). Tendríamos más ligaduras que ecuaciones. El sistema sería matemáticamente indeterminado desde la Dinámica Newtoniana de sistemas ideales.
Para evitar el problema anterior, en los diseños se anulan deliberadamente una de las reacciones axiales:
- Gozne 1 (p.ej., el superior): Se diseña como un «gozne de empuje» (o rodamiento de empuje). Fija la posición radial (X, Y) y también la axial (Z).
- Gozne 2 (p.ej., el inferior): Se diseña como un «gozne radial» (o rodamiento simple). Fija la posición radial (X, Y), pero permite que el eje se deslice libremente en la dirección Z.
Esto es un diseño isostático. La única diferencia física entre las dos configuraciones (empuje superior vs. empuje inferior) es cómo se carga el eje:
- Empuje Superior: El peso del cuerpo «cuelga» del gozne superior y el eje está sometido a tensión.
- Empuje Inferior: El peso descansa sobre el gozne inferior y el eje está sometido a compresión.
Precesión giroscópica según un observador no inercial
Desde el sistema de referencia centrado en el cuerpo, un giróscopo equilibrado previamente, girando con velocidad angular de espín ω y con una carga adicional, tiende a subir con una velocidad instantánea de traslación u causada por el momento del peso extra. Desde el sistema de referencia inercial, el giróscopo tiende a caer pero la relatividad entre marcos de referencia produce la velocidad relativa ascendente. La fuerza de inercia de Coriolis (-2 ω x u) resulta ser lateral al vector ω, y ello produce el comienzo de la precesión Ω en el sentido antihorario.
En una segunda fase, desde el sistema de referencia centrado en el eje vertical de precesión, la fuerza de inercia de Coriolis (-2 Ω x v) debida al movimiento de rotación de espín de cada punto material del giróscopo, produce un par de fuerzas horizontales (a lo largo de la flecha del giróscopo) que contrarresta el momento del peso extra. Esto produce la precesión uniforme, regulándose la propia velocidad de precesión Ω. A diferencia de la fuerza de inercia de Coriolis de arranque, ésta otra fuerza de Coriolis es distribuida, siendo máxima en los puntos extremos superior e inferior del giróscopo.
La primera fuerza de Coriolis acelera (frena) la precesión y a continuación, la segunda fuerza de Coriolis la frena (acelera).
Si se perturba ligeramente el giróscopo en precesión, mediante un impulso bien vertical como lateral, se observa la nutación:
- Si empujas hacia abajo, el giróscopo acelera.
- Esta aceleración (Ω más rápida) lo hace subir.
- Al subir, frena.
- Al frenar (Ω más lenta), empieza a caer.
Esto produce una oscilación («cabeceo») que se superpone al movimiento suave de la precesión. La nutación es la reacción del giróscopo a las perturbaciones de su estado de equilibrio. Cuando la perturbación es muy pequeña, la nutación es senoidal. Pero, según las condiciones iniciales de la perturbación, la nutación puede ser ondulada o cuspidal. Cuando el golpe es vertical, domina la primera fuerza de Coriolis y la punta de la flecha del giróscopo traza un camino con «puntos angulosos». Cuando el empujón es lateral, domina el momento giroscópico y la flecha traza «rizos».
La nutación es el resultado de combinar dos movimientos de rotación como la cicloide (trocoides) es el resultado de combinar un movimiento de rotación y uno de traslación. De ahí que tengan comportamientos cualitativos tan parecidos.
Conservación de la masa/carga eléctrica en un sistema físico cerrado
La inercia es una propiedad intrínseca de la materia y se cuantifica con la masa. Un sistema físico, que no intercambia materia con su exterior, tiene una masa total que no cambia con el tiempo, y por tanto se conserva. Si el sistema tiene partes diferenciadas, es la suma de las masas lo que se conserva. Pero si no existe intercambio de materia entre partes, se conserva la masa de cada parte. En un sistema de dos cuerpos se puede definir la masa total como la masa reducida, que representa la inercia puesta en juego durante el movimiento relativo entre cuerpos.
La carga eléctrica es otra propiedad intrínseca de la materia. La misma lógica se aplica con la carga eléctrica total del sistema pero sustituyendo intercambio de materia por contacto eléctrico que permite trasvase de carga. La carga eléctrica total de un sistema aislado eléctricamente se conserva.
Relación física a tres
El principio 0 de la Termodinámica establece que si dos cuerpos están en equilibrio térmico con un tercer cuerpo, entonces están en equilibrio térmico entre sí, lo que significa que los tres cuerpos tendrán la misma temperatura. La misma lógica se puede aplicar al equilibrio de presiones y químico.
Si el evento A ocurre antes que el evento B, y el evento B ocurre antes que el evento C, entonces A ocurre antes que C.
Si dos vectores físicos son perpendiculares con un tercero, no tienen por qué ser perpendiculares entre sí.
La primera y segunda son relaciones lógicas transitivas (equilibrios termodinámicos y causalidad). Cualquier relación basada en la comparación de una propiedad física escalar es transitiva.
Si un conjunto de vectores (no nulos) es ortogonal, entonces está garantizado que es linealmente independiente. Es imposible construir un vector del conjunto como una combinación de los otros si todos son perpendiculares entre sí. Aunque un conjunto de vectores no necesita ser ortogonal para ser linealmente independiente.