Dentro de un cilindro hueco abierto por su extremo superior tenemos un clavo de hierro que se puede mover libremente dentro del cilindro. En el extremo superior abierto del cilindro colocamos un imán. Imán y clavo están a una distancia suficiente como para no atraerse y moverse por ello. De repente dejamos caer el conjunto, liberados de ligaduras tanto el cilindro como el clavo (aunque éste estuviera en contacto con la base del cilindro). Rápidamente, el conjunto clavo-cilindro cae solidario pues el clavo es atraído al imán provocando la unión de ambos. ¿Por qué? El cilindro con el imán sufre dos fuerzas a favor de la caída (peso y fuerza de atracción magnética) mientras que el clavo sufre el peso a favor de la caída y la fuerza de atracción magnética en sentido opuesto a la caída. Tras un tiempo, las aceleraciones de ambos se diferencian lo suficiente como para acercarse durante la caída y unirse.
Rozamiento estático e inercia, ¿se confunden en la práctica?
El rozamiento estático es la resistencia al movimiento relativo incipiente entre cuerpos. La inercia es la resistencia a cambiar de estado de movimiento de un cuerpo. Para que se manifiesten debe existir tentativa al movimiento relativo o cambio de movimiento, respectivamente. Si un cuerpo apoyado se resistiera a moverse por acción de una fuerza deliberada, ¿cómo sabremos si es por su inercia (masa) o por el rozamiento estático con el apoyo? Para mover cualquier cuerpo desde el reposo se requiere de un impulso finito (fuerza neta positiva integrada en el tiempo) que dependerá de la masa a priori (cantidad de movimiento inicial). El rozamiento estático máximo depende de la reacción de apoyo, que de alguna manera puede depender del peso del cuerpo (masa gravitatoria) aunque no siempre. Como vemos, es difícil desacoplar inercia de rozamiento estático en cuerpos que tienden al movimiento incipiente. Es más sencillo con cuerpos en movimiento manifiesto. Supongamos un cuerpo trazando una curva. La propia inercia del cuerpo justifica la tentativa a salirse por la tangente y con ella, la aparición del rozamiento estático en dirección normal a la curva. Como vemos, la inercia origina el rozamiento estático pero la velocidad máxima de trazado de curva NO depende de la masa del cuerpo y sí del coeficiente de rozamiento estático.
Tres esferas de igual área y forma, pero diferente masa, se cuelgan respectivamente de tres cuerdas idénticas en aire en calma (viscosidad pequeña, flujo laminar). Se desplazan la misma amplitud A (por debajo de 20º), se sueltan y se observa que la esfera más liviana se detiene antes y la más pesada, la última. ¿Cuál es el motivo? El diferente coeficiente es β=b/(2*inercia) donde b es un parámetro que depende de la viscosidad del medio y de la geometría del cuerpo. Si se desplazara cada esfera distinta amplitud, de manera que el producto inercia*A² (energía) fuera constante, ¿se lograría teóricamente igualar los tiempos de frenado? No. Siempre llegará teóricamente antes al reposo la esfera más ligera y más tarde la esfera más pesada.
Potencia, ¿trabajo o energía por unidad de tiempo?
La potencia mecánica consumida por una determinada fuerza es su trabajo elemental por unidad de tiempo infinitesimal o también la derivada temporal del trabajo realizado (integral) por dicha fuerza en una trayectoria dada (y con ella, en un tiempo dado). La potencia eléctrica también se define como el trabajo elemental eléctrico (de origen electrostático o no) consumido por unidad de tiempo infinitesimal. Sólo para el caso de movimiento de cuerpos (cargas), la potencia instantánea se puede escribir como el producto escalar de fuerza por velocidad. La derivada temporal de la energía mecánica NO es la potencia mecánica total. Numéricamente, la derivada temporal de la energía mecánica puede coincidir con una de las potencias consumidas (normalmente por fuerzas disipativas).
Un medio material se puede modelar como un conjunto de osciladores armónicos ACOPLADOS. En ese modelo, la energía mecánica de cada oscilador no es constante. La potencia de una onda mecánica, que nunca transporta materia aunque se origina por el movimiento local del medio, es la derivada de la energía mecánica local de un elemento infinitesimal del medio (un oscilador armónico) por el que se propaga la onda. En medios no absorbentes y ondas progresivas, esta potencia se conserva punto a punto y en ondas finitas (pulsos), la potencia se propaga con la onda.
Ambas potencias se miden en W.
Medida indirecta de la aceleración tangencial
Si dividimos la potencia consumida por el objeto en su movimiento (trabajo realizado por la fuerza neta externa) por el módulo de su cantidad de movimiento, tenemos la aceleración tangencial. ¿Movimientos circulares uniformes no consumen potencia? Dicho así…. En la realidad, para mantener un movimiento circular uniforme, hay que aplicar una fuerza centrípeta constante a la vez que imprimir una velocidad inicial tangente. Lo primero requiere de un momento motriz ininterrumpido, de ahí que la potencia externa necesaria para que el objeto siga describiendo el MCU sea igual al par-motor por la velocidad de giro.
Fuerzas centrales y ley de reflexión
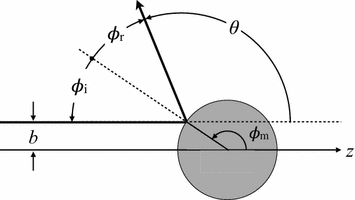
La dispersión elástica consiste en el desvío de la trayectoria de un proyectil que se acerca desde el infinito (MRU) a un blanco estático con el que interacciona y se aleja con la misma energía (velocidad y MRU) pero diferente dirección. Es la versión microscópica (interacción a distancia) de un choque (contacto) entre proyectil y blanco. En los sistemas gobernados por interacciones centrales, el momento lineal se conserva en el punto de máximo acercamiento al blanco, lo que se traduce en que los ángulos de incidencia y de salida del proyectil en el punto de máximo acercamiento (ápside) al blanco, medidos con respecto a la dirección radial que pasa por el blanco y el ápside, resultan iguales. Esto evoca la ley de reflexión de la Óptica y la teoría ondulatoria. Se trata de un comportamiento más común de lo que parece. En ondas electromagnéticas, es sabido que en las fronteras descargadas, la componente tangencial del campo eléctrico (central) no cambia (i.e. es continua) entre medios mientras que en fronteras sin corrientes eléctricas, es la componente normal del campo magnético (no central) la que resulta continua.